3月25日12时,《张朝阳的物理课》第二百四十一期开播,搜狐创始人、董事局主席兼CEO、物理学博士张朝阳坐镇搜狐视频直播间,为观众解答这一疑问。本节课首先回顾了张量分析中对偶基矢的定义以及逆变指标和协变指标的含义,然后通过用对偶基矢定义了度规和克氏符,并证明了这样的度规具有升降指标功能,最后推导出克氏符的度规表达式,与教科书上的计算公式一致,且更具有直观的几何含义。
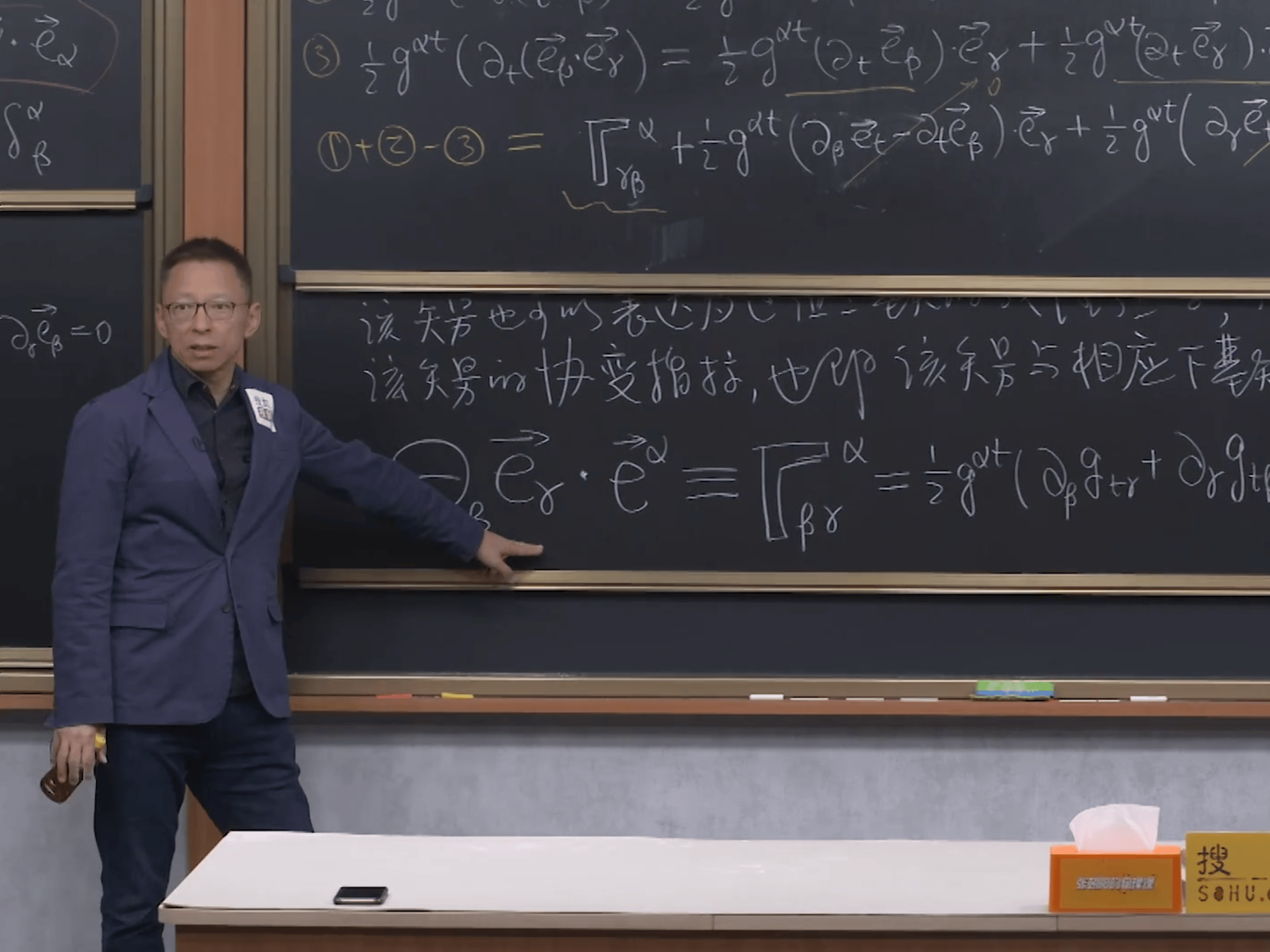
对偶基矢和度规
对于一个线性空间,无论它的维数是多少,人们总可以找到一组线性无关的基矢e_α,将其中的任意矢量V表示成
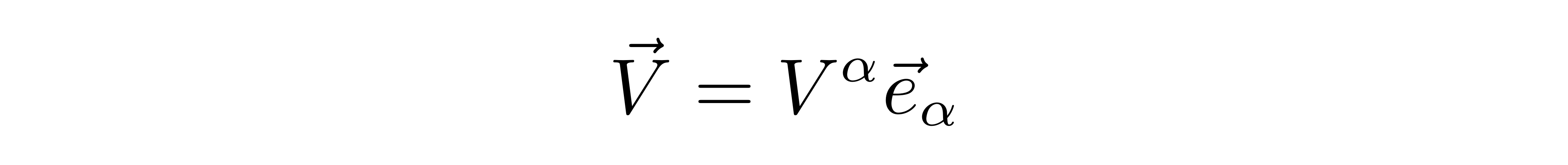
其中α的数量就是空间的维度,V^α称为矢量V的逆变分量。由于我们把α指标写在基矢e的下边,因此称这组基矢为下基矢。与此同时,我们还可以在这个空间里找到另外一组基矢,我们用带有上指标的符号e^β来表示,称为上基矢。由于下基矢是线性无关的,所以总可以找到与之对偶的上基矢。所谓对偶,指的是上下基矢满足
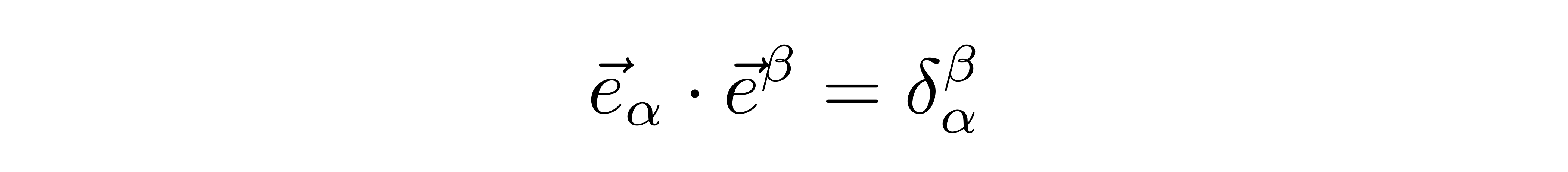
有了这样一组上基矢后,我们还可以把矢量表示成
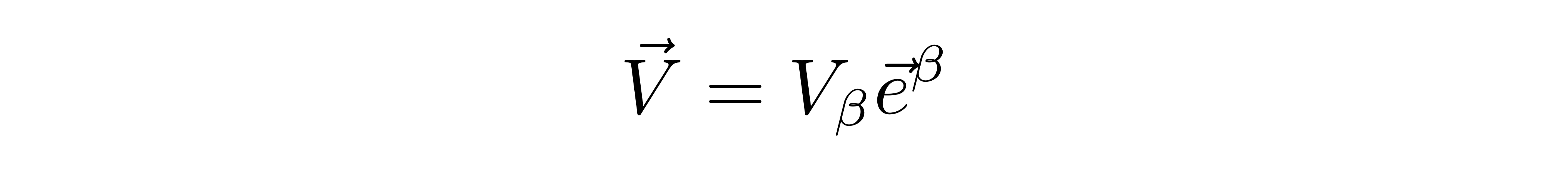
这里的V_β就被称为矢量V的协变分量。
我们还可以计算矢量V和这些基矢的内积,它们分别是
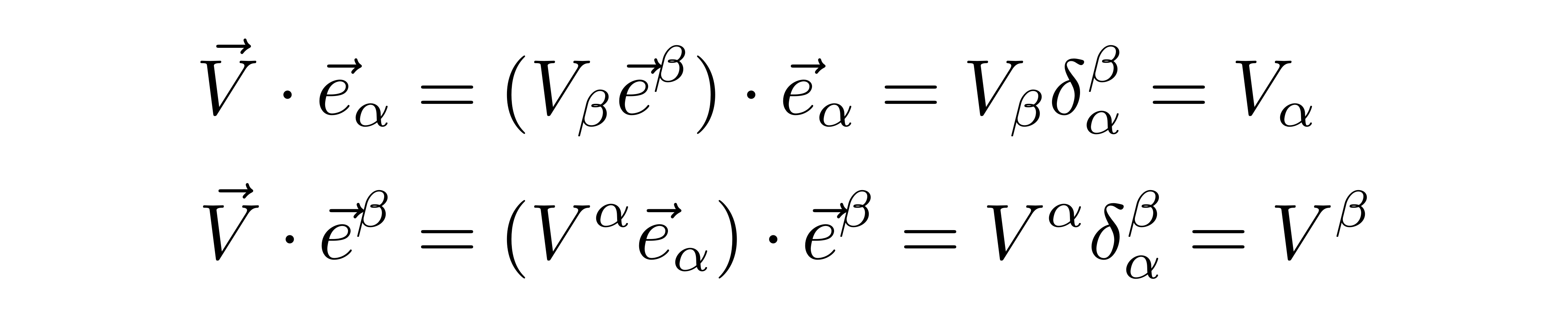
这些计算说明:矢量V的逆变分量V^α既是矢量展开成下基矢的线性组合的组合系数,也是该矢量与相应指标的上基矢的内积,协变分量V_β既是矢量展开成上基矢的线性组合的组合系数,也是该矢量与相应指标的下基矢的内积。
我们在构造基矢的时候要求了上下基矢的内积等于克罗内克δ,但并没有要求上基矢的两两内积和下基矢的两两内积分别等于多少。由于这些内积的值是由两个携带分量指标的矢量计算出来的,我们可以把它们视为一个二阶张量的不同分量,记为
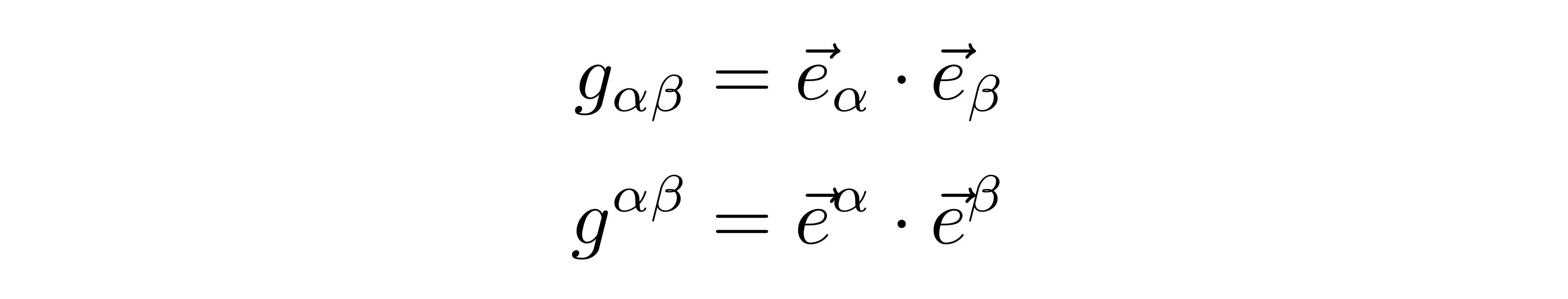
这个二阶张量就被称为度规,分别称g_αβ和g^αβ为协变度规和逆变度规。如果将逆变度规与上基矢缩并,也就是做如下所示的运算

运算到这一步,我们需要认识到,基矢e_α虽然带一个指标,但那并不是表示分量的指标,而只是标记它是第几个基矢。基矢本身就是一个矢量,也就是可以用一个不带指标的符号来标记
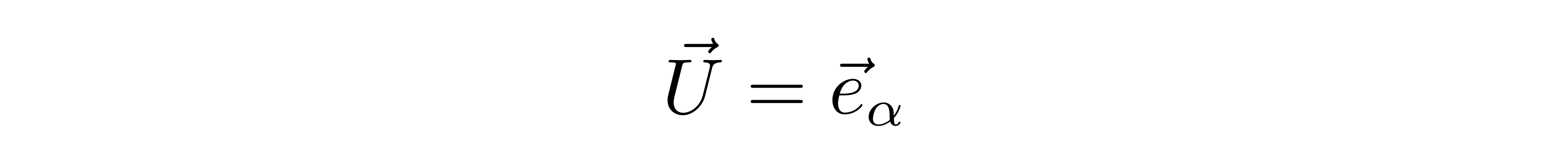
那么它与下基矢e_β进行内积运算后也会像一般的矢量那样得到其协变分量,再与上基矢e^β缩并后,就又得到了矢量自身
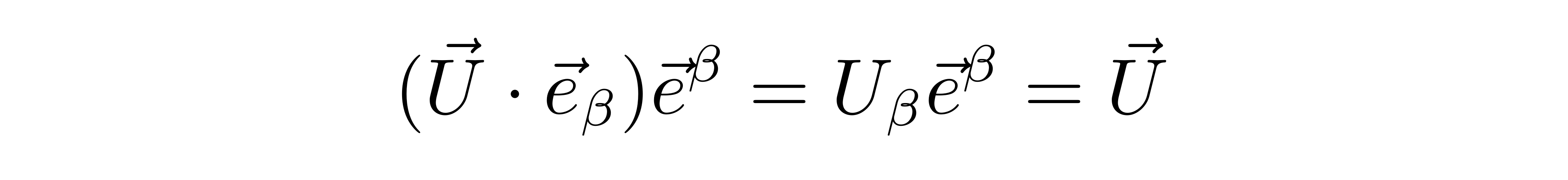
将U换回下基矢,就是
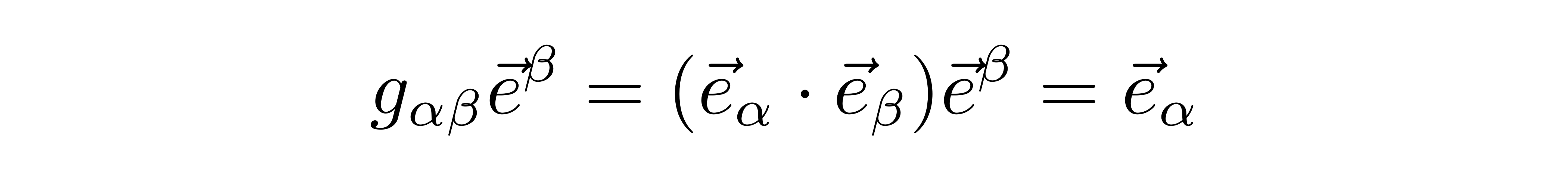
从这里可以看到,逆变度规和上基矢缩并后会得到下基矢。类似地,可以得到
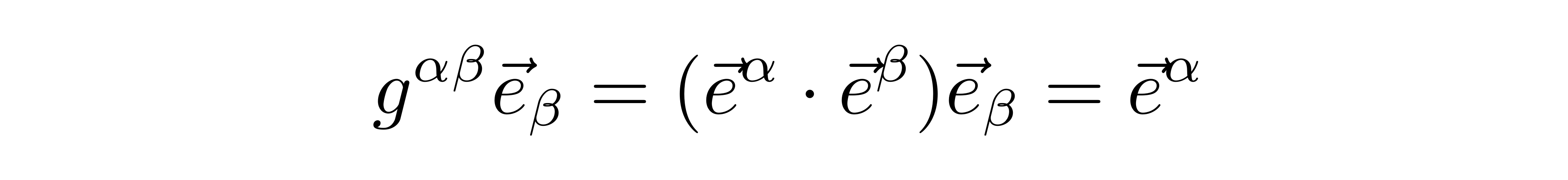
由此,我们可以发现,度规具有互换对偶基矢的功能。类似地,还可以发现协变度规和逆变度规满足互逆的关系
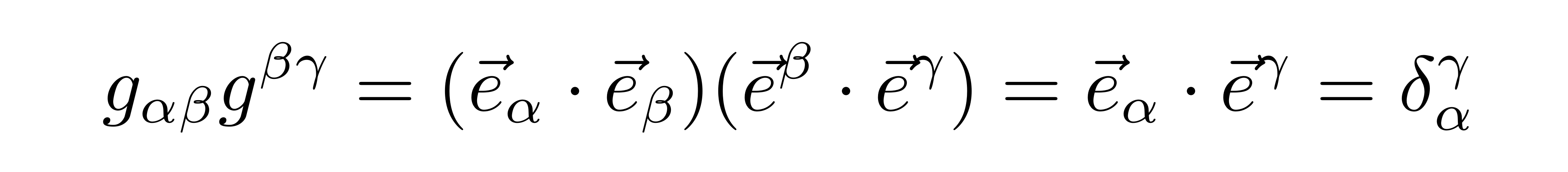
以及,度规具有升降张量指标的功能
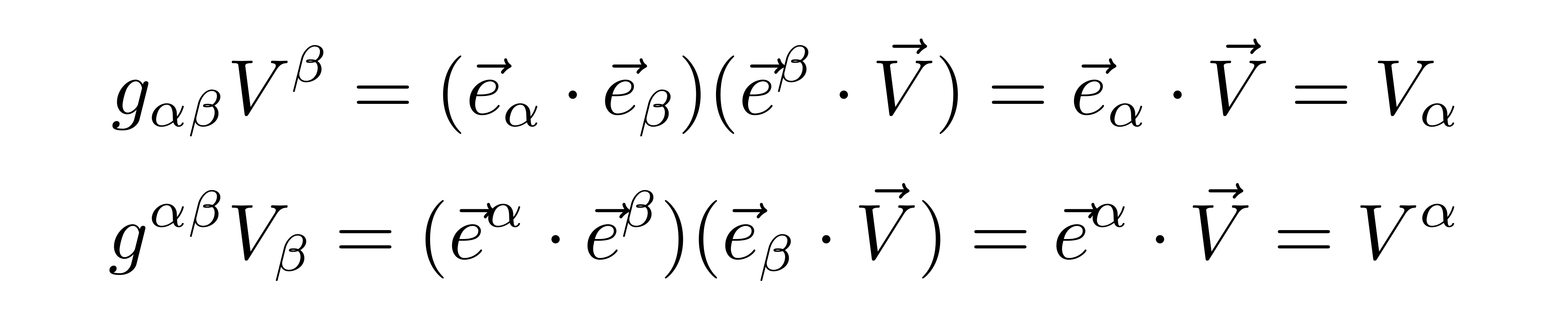
协变导数和克氏符
在矢量微积分中,一个矢量关于坐标的偏导数包含矢量分量的偏导和基矢的偏导,如果考虑这个偏导数的逆变分量,可以得到
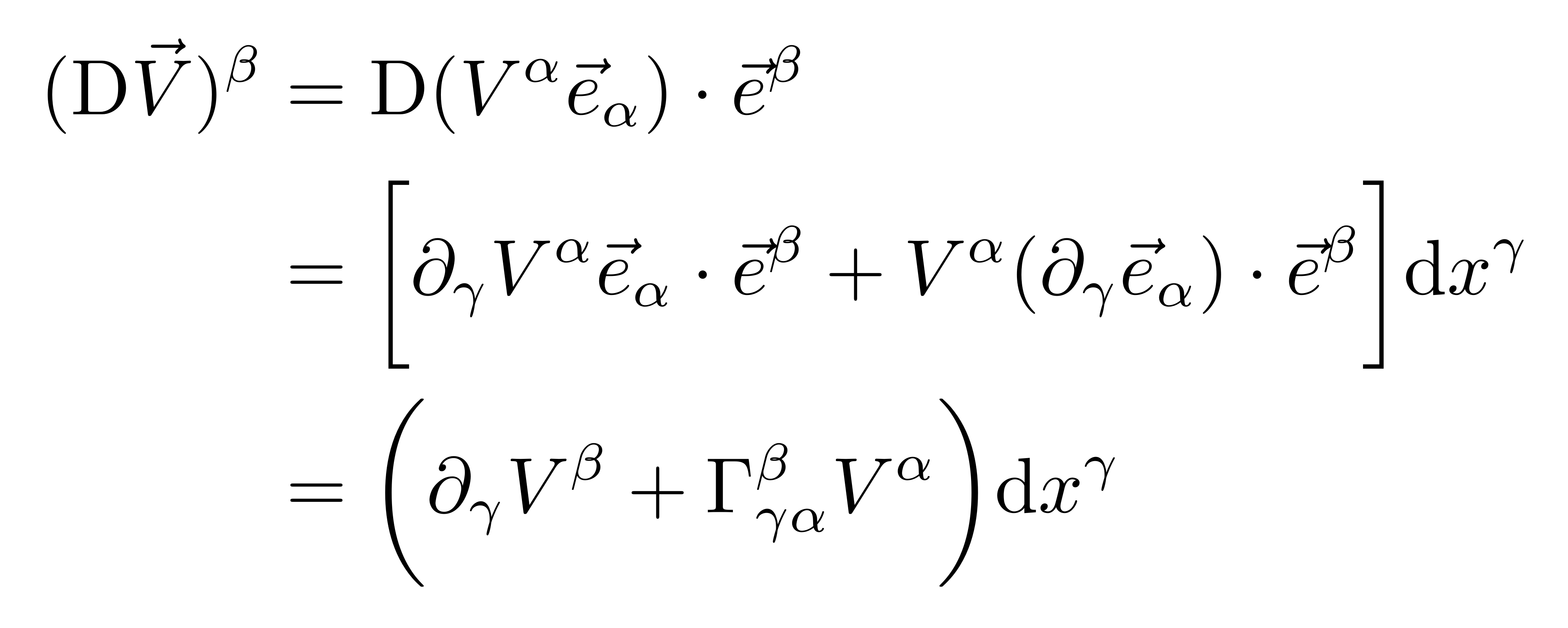
其中定义了克氏符
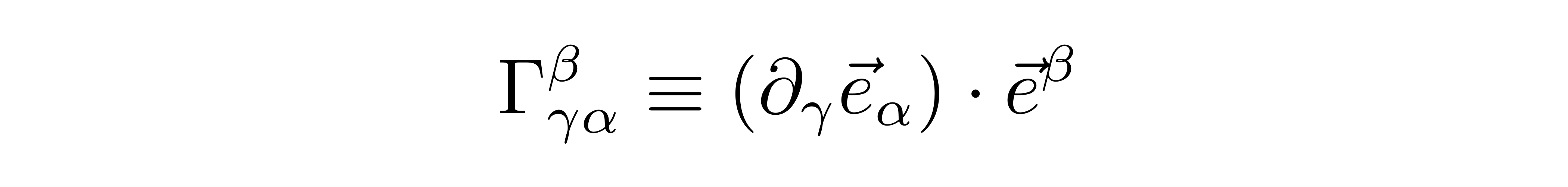
如果采用的是坐标基矢,也就是基矢是由位置矢量对坐标的偏导来定义的
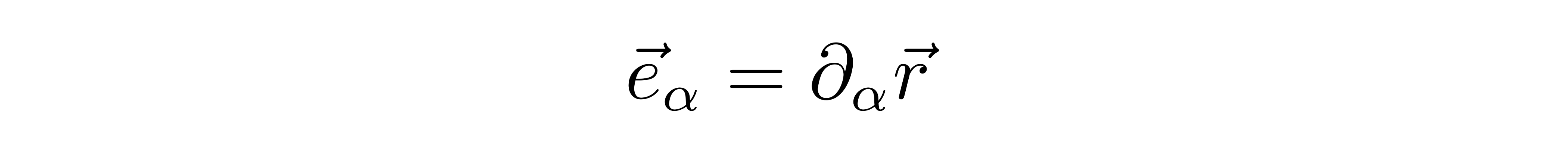
那么
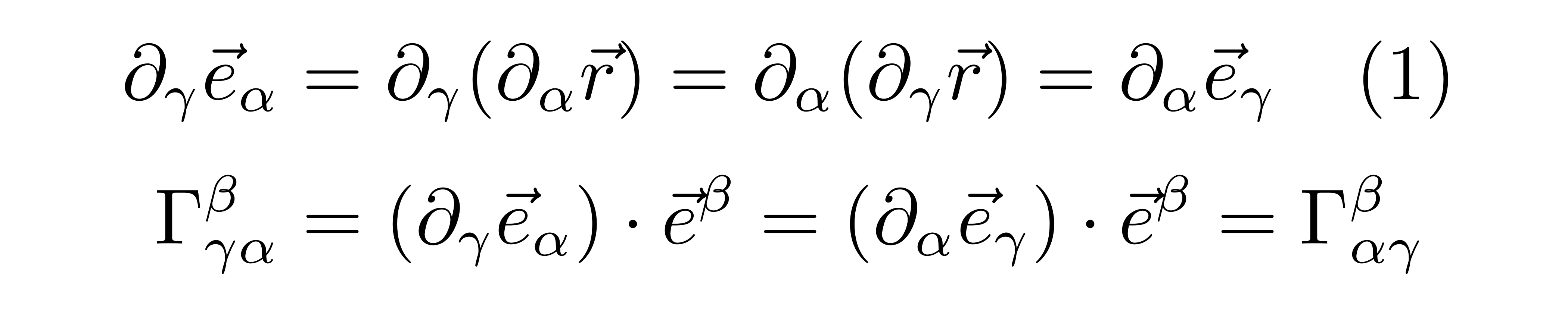
也就是克氏符的两个下指标是对称的。需要声明的是,以上的偏导运算必须是在平直空间中进行的,当我们把这些结论用在弯曲空间中时,需要把弯曲空间等距地嵌入到高维平直空间后才能进行。以二维单位球面为例,我们需要把它嵌入到三维平直空间中,才能对矢量做合法的偏导运算,例如对于极角方向的坐标基矢,对极角求偏导后会得到垂直于二维球面的矢量
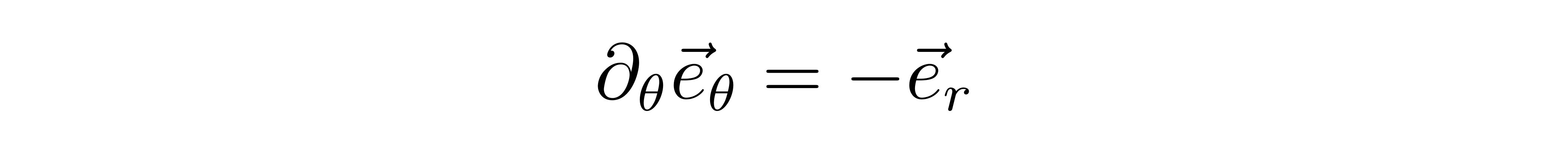
再将这一矢量与二维球面中的上基矢分别内积,就可以用这种方法得出相应的克氏符
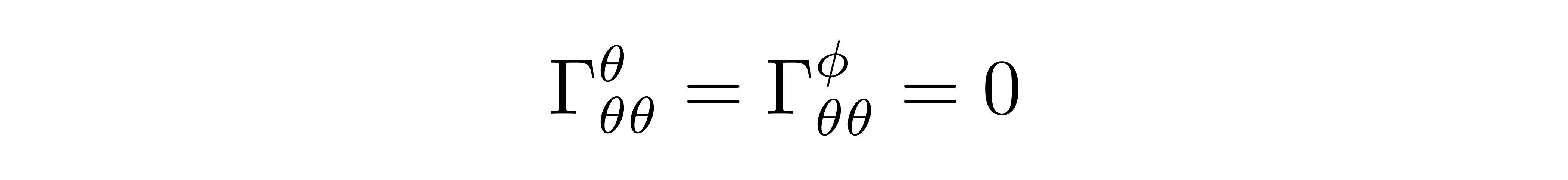
也正是因为这一运算已经是在高维平直空间中进行的,所以在(1)式的第二个等号中我们可以交换两次求偏导的顺序。如果回到低维弯曲空间中来看,这对应了“空间的挠率为零”这一性质。
对于矢量偏导的协变分量,可以得到
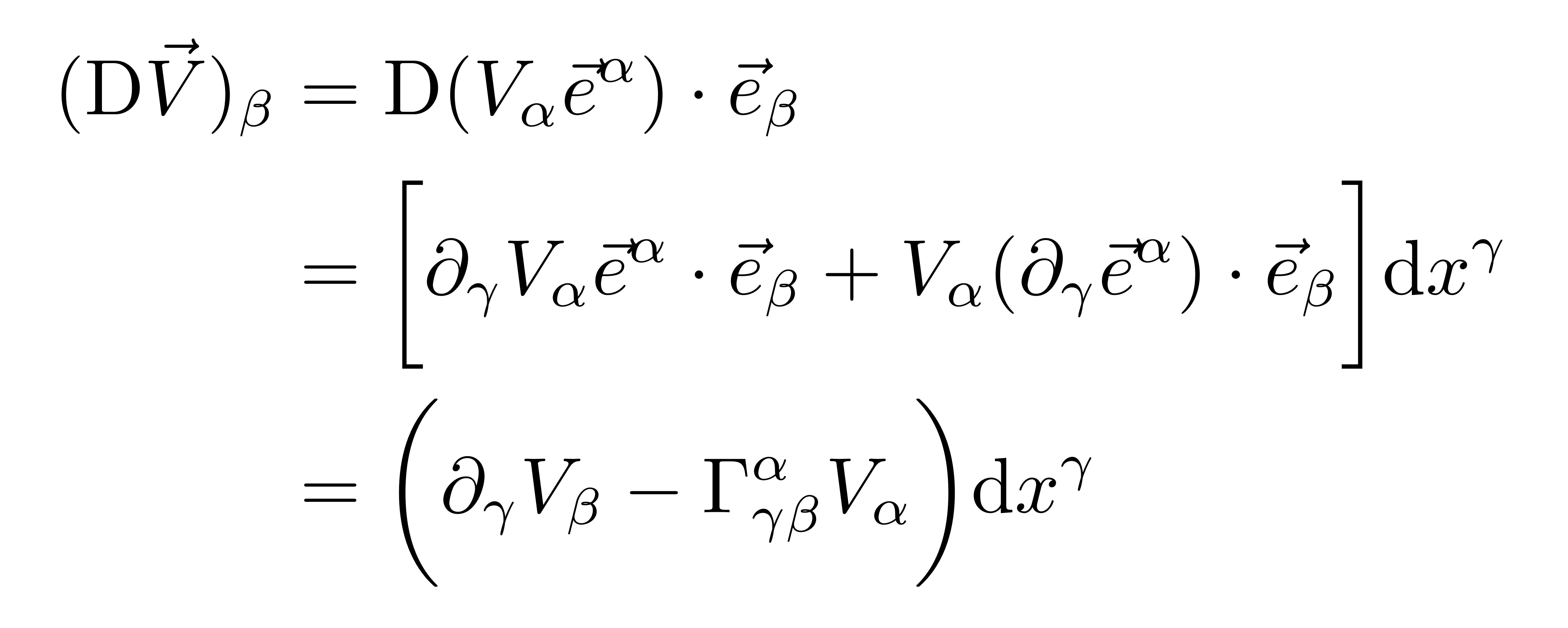
最后一步用到了上下基矢互为对偶的性质
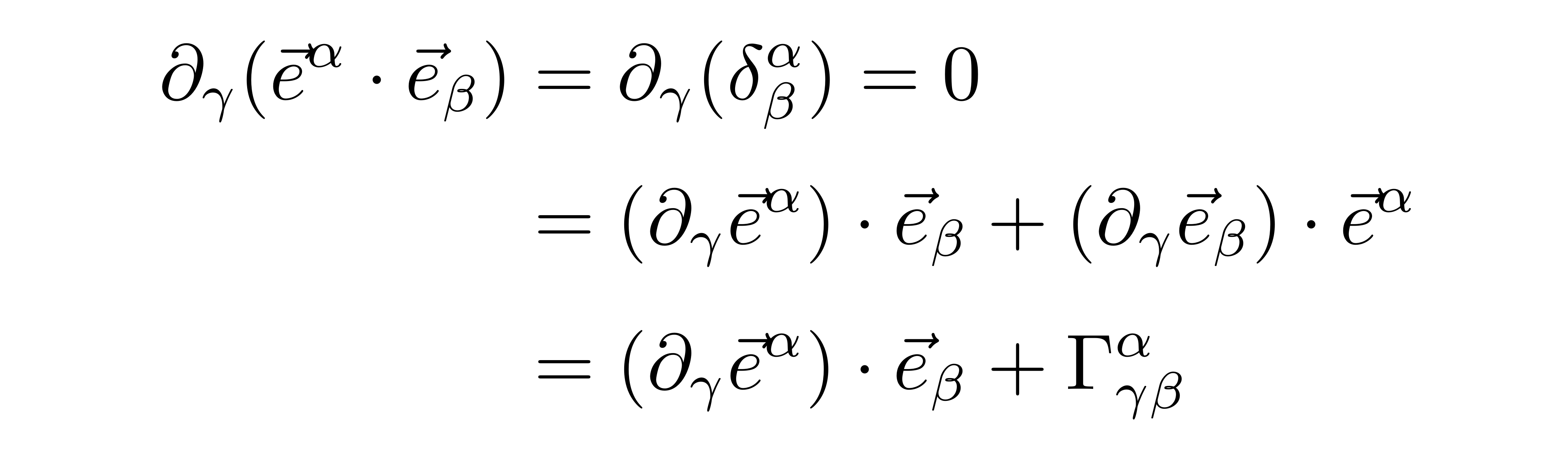
克氏符的度规表达式
在之前的课中,我们介绍过度规的计算公式
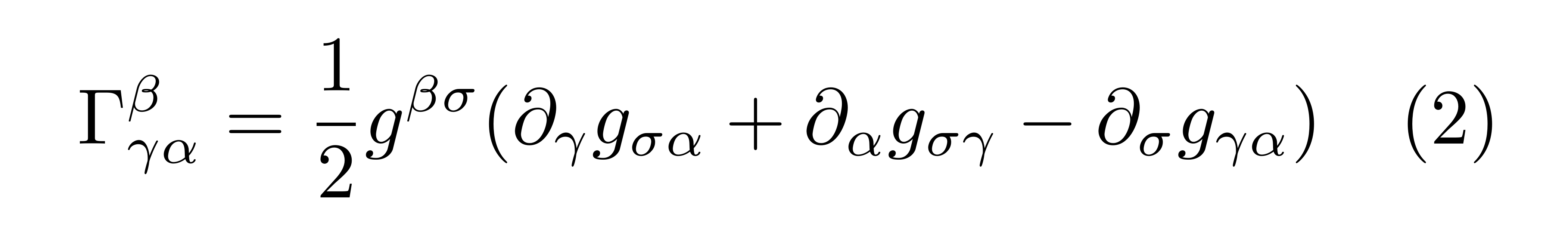
它可以由度规的协变散度为0推导出来。因为这个公式避免了对矢量求偏导,所以可以很方便地在弯曲空间中直接运算。本节课我们将说明,这个计算公式和上一节用矢量微积分导出的克氏符表达式是等价的。为了证明这一点,需要将度规用基矢的内积代入,对于上式三项分别得到

将上述三项组合回去,得到
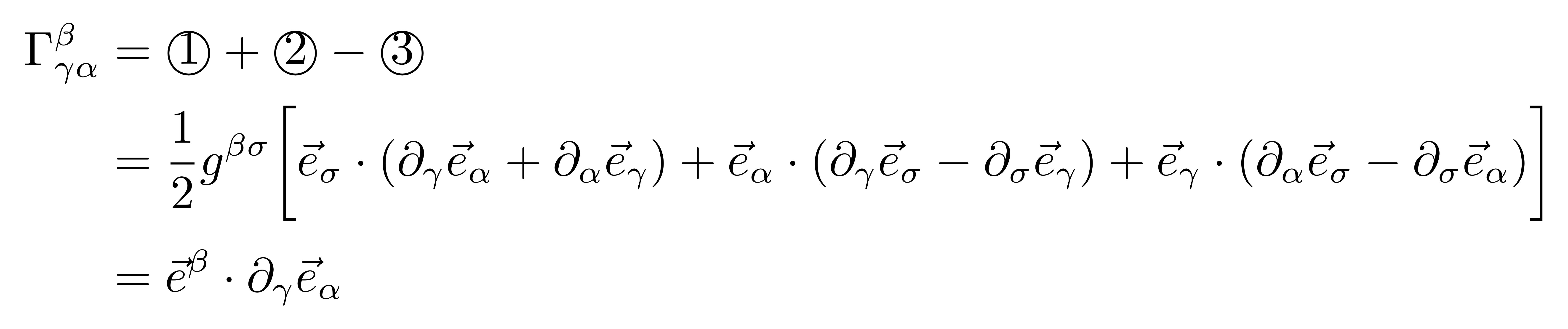
其中再次利用了(1)式交换了基矢和偏导的两个指标。这样就说明了用计算公式(2)所得到的结果正是我们借助矢量微积分所定义的克氏符。
据了解,《张朝阳的物理课》于每周周日中午12时在搜狐视频直播,网友可以在搜狐视频APP“关注流”中搜索“张朝阳”,观看直播及往期完整视频回放;关注“张朝阳的物理课”账号,查看课程中的“知识点”短视频;此外,还可以在搜狐新闻APP的“搜狐科技”账号上,阅览每期物理课程的详细文章。



 微信扫一扫打赏
微信扫一扫打赏
 支付宝扫一扫打赏
支付宝扫一扫打赏






